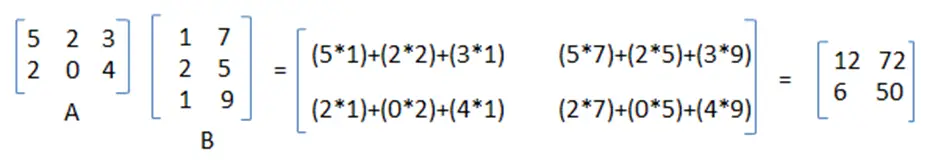Here you get encryption and decryption program for hill cipher in C and C++.
What is Hill Cipher?
In cryptography (field related to encryption-decryption) hill cipher is a polygraphic cipher based on linear algebra. Invented by Lester S. Hill in 1929 and thus got it’s name. It was the first cipher that was able to operate on 3 symbols at once.
Also Read: Caesar Cipher in C and C++ [Encryption & Decryption]
Encryption: The given message string and key string is represented in the form of matrix. Then key and message matrix are multiplied. Finally modulo 26 is taken for each element of matrix obtained by multiplication. The key matrix that we take here should be invertible, otherwise decryption will not be possible.
Decryption: The encrypted message matrix is multiplied by the inverse of key matrix and finally its modulo 26 is taken to get the original message.
To learn more about hill cipher you can visit following link.
https://en.wikipedia.org/wiki/Hill_cipher
Hill Cipher Program in C
#include<stdio.h>
#include<math.h>
float encrypt[3][1], decrypt[3][1], a[3][3], b[3][3], mes[3][1], c[3][3];
void encryption(); //encrypts the message
void decryption(); //decrypts the message
void getKeyMessage(); //gets key and message from user
void inverse(); //finds inverse of key matrix
void main() {
getKeyMessage();
encryption();
decryption();
}
void encryption() {
int i, j, k;
for(i = 0; i < 3; i++)
for(j = 0; j < 1; j++)
for(k = 0; k < 3; k++)
encrypt[i][j] = encrypt[i][j] + a[i][k] * mes[k][j];
printf("\nEncrypted string is: ");
for(i = 0; i < 3; i++)
printf("%c", (char)(fmod(encrypt[i][0], 26) + 97));
}
void decryption() {
int i, j, k;
inverse();
for(i = 0; i < 3; i++)
for(j = 0; j < 1; j++)
for(k = 0; k < 3; k++)
decrypt[i][j] = decrypt[i][j] + b[i][k] * encrypt[k][j];
printf("\nDecrypted string is: ");
for(i = 0; i < 3; i++)
printf("%c", (char)(fmod(decrypt[i][0], 26) + 97));
printf("\n");
}
void getKeyMessage() {
int i, j;
char msg[3];
printf("Enter 3x3 matrix for key (It should be inversible):\n");
for(i = 0; i < 3; i++)
for(j = 0; j < 3; j++) {
scanf("%f", &a[i][j]);
c[i][j] = a[i][j];
}
printf("\nEnter a 3 letter string: ");
scanf("%s", msg);
for(i = 0; i < 3; i++)
mes[i][0] = msg[i] - 97;
}
void inverse() {
int i, j, k;
float p, q;
for(i = 0; i < 3; i++)
for(j = 0; j < 3; j++) {
if(i == j)
b[i][j]=1;
else
b[i][j]=0;
}
for(k = 0; k < 3; k++) {
for(i = 0; i < 3; i++) {
p = c[i][k];
q = c[k][k];
for(j = 0; j < 3; j++) {
if(i != k) {
c[i][j] = c[i][j]*q - p*c[k][j];
b[i][j] = b[i][j]*q - p*b[k][j];
}
}
}
}
for(i = 0; i < 3; i++)
for(j = 0; j < 3; j++)
b[i][j] = b[i][j] / c[i][i];
printf("\n\nInverse Matrix is:\n");
for(i = 0; i < 3; i++) {
for(j = 0; j < 3; j++)
printf("%d ", b[i][j]);
printf("\n");
}
}
Hill Cipher Program in C++
#include<iostream>
#include<math.h>
using namespace std;
float encrypt[3][1], decrypt[3][1], a[3][3], b[3][3], mes[3][1], c[3][3];
void encryption(); //encrypts the message
void decryption(); //decrypts the message
void getKeyMessage(); //gets key and message from user
void inverse(); //finds inverse of key matrix
int main() {
getKeyMessage();
encryption();
decryption();
}
void encryption() {
int i, j, k;
for(i = 0; i < 3; i++)
for(j = 0; j < 1; j++)
for(k = 0; k < 3; k++)
encrypt[i][j] = encrypt[i][j] + a[i][k] * mes[k][j];
cout<<"\nEncrypted string is: ";
for(i = 0; i < 3; i++)
cout<<(char)(fmod(encrypt[i][0], 26) + 97);
}
void decryption() {
int i, j, k;
inverse();
for(i = 0; i < 3; i++)
for(j = 0; j < 1; j++)
for(k = 0; k < 3; k++)
decrypt[i][j] = decrypt[i][j] + b[i][k] * encrypt[k][j];
cout<<"\nDecrypted string is: ";
for(i = 0; i < 3; i++)
cout<<(char)(fmod(decrypt[i][0], 26) + 97);
cout<<"\n";
}
void getKeyMessage() {
int i, j;
char msg[3];
cout<<"Enter 3x3 matrix for key (It should be inversible):\n";
for(i = 0; i < 3; i++)
for(j = 0; j < 3; j++) {
scanf("%f", &a[i][j]);
c[i][j] = a[i][j];
}
cout<<"\nEnter a 3 letter string: ";
cin>>msg;
for(i = 0; i < 3; i++)
mes[i][0] = msg[i] - 97;
}
void inverse() {
int i, j, k;
float p, q;
for(i = 0; i < 3; i++)
for(j = 0; j < 3; j++) {
if(i == j)
b[i][j]=1;
else
b[i][j]=0;
}
for(k = 0; k < 3; k++) {
for(i = 0; i < 3; i++) {
p = c[i][k];
q = c[k][k];
for(j = 0; j < 3; j++) {
if(i != k) {
c[i][j] = c[i][j]*q - p*c[k][j];
b[i][j] = b[i][j]*q - p*b[k][j];
}
}
}
}
for(i = 0; i < 3; i++)
for(j = 0; j < 3; j++)
b[i][j] = b[i][j] / c[i][i];
cout<<"\n\nInverse Matrix is:\n";
for(i = 0; i < 3; i++) {
for(j = 0; j < 3; j++)
cout<<b[i][j]<<" ";
cout<<"\n";
}
}Output

Comment below if you have any queries related to above program for hill cipher in C and C++.
The post Hill Cipher in C and C++ (Encryption and Decryption) appeared first on The Crazy Programmer.